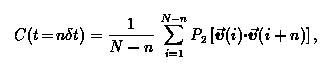
In the present article we model benzene orientational randomization (BOR) at infinite dilution in Na-Y (Si:Al>=2.0). Below we describe various structural and physical assumptions of our model, in addition to the kinetic simulation techniques used to perform the ensemble average in Eq.(0.2). We then summarize the theoretical methodology at the end of this Section.
Benzene mobility in Na-Y strongly depends upon the number and placement of Na(II) cations in the zeolite framework structure. It is therefore important when discussing benzene mobility in a particular Na-Y to quantify the Na(II) occupancy, in addition to standard properties such as the Si:Al ratio. For example, a Si:Al ratio of 2.0 requires 64 ions per unit cell to balance the negative framework charge. In this case we assume full occupation of Na sites I' (32 per unit cell, located in smaller beta cages) and Na sites II (32 per unit cell, 4 per supercage on the vertices of a tetrahedron). This occupancy model is reasonable considering that only the Na(II) ions are accessible to a penetrant the size of benzene. In addition, iffraction studies of Na-Y (Si:Al=1.7) and Na-Y (Si:Al=2.4) find nearly full Na(II) occupation. Before discussing Na(II) occupancy models for other Si:Al ratios, we describe the binding sites, hopping paths and kinetic simulation techniques used to calculate the OCF for benzene in Na-Y (Si:Al=2.0).
Our previous MD-DOCKER calculations find two distinct binding sites for benzene in Na-Y (Si:Al=2.0), in agreement with the powder neutron diffraction results of Fitch et al. The calculated sorption sites are shown in Fig. 2. In the SII binding site, benzene is facially coordinated to a supercage 6-ring, 2.70 angstroms above Na(II). In the W site, benzene is centered in the 12-ring window, 5.3 angstroms from the SII site. Because of the strong Na-benzene interaction, the SII site is much more stable than the W site, by ca. 25 kJ mol-1 according to some estimates.
For benzene in Na-Y (Si:Al=2.0), the calculated SII<->SII and SII<->W minimum energy paths (MEPs) are shown in Figs. 3 and 5 with the corresponding energetics shown in Figs. 4 and 6, respectively. These MEPs were obtained using our coordinate driving method with our recently fitted potential energy surface for benzene in faujasites. These hopping paths clearly demonstrate the reorientation processes probed by NMR relaxation and two-dimensional exchange NMR. The calculated SII->SII activation energy is 35 kJ mol-1 obtained by NMR relaxation (vide infra).
We apply the kinetic Monte Carlo (KMC) algorithm to benzene mobility in Na-Y by replacing the zeolite framework with a three-dimensional lattice of SII and W binding sites. Such a lattice model is known to accurately reproduce mobilities when site residence times are much longer than travel times between sites. This is indeed the case for benzene in cation-containing faujasites because of the strong charge-quadrupole interactions between Na(II) ions and benzene. Connecting the SII and W sites are four distinct hopping events, each with a characteristic rate coefficient: k(SII->SII, k(SII->W), k(W->SII) and k(W->W). The probability to make a particular hop is proportional to the associated rate coefficient.
We use a fixed time step KMC algorithm for OCF calculations in which a random hop is attempted at each time step. The hop is accepted or rejected based on the kinetic Metropolis prescription in which a ratio of hopping rate coefficients, khop/kref, is compared to a random number. Here kref is a reference rate that controls the temporal resolution of the calculated OCF, i.e. dt = 1/kref is the time bin width used for accumulating KMC statistics. During a KMC simulation benzene's orientation is stored at each time step i = 1, ...,N. The OCF is calculated as:
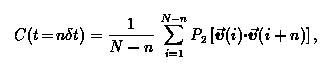
where v(i) is the unit vector specifying the orientation at KMC step i. We note that calculating well converged OCFs for long times is computationally challenging because of the difficulty in obtaining proper cancellation of positive and negative P2(x) values from a Monte Carlo random walk.
We use a variable time step KMC algorithm for mean square displacement calculations in which a hop is made every KMC step and the system clock is updated accordingly. The mean time elapsed before each hop is the inverse of the total rate coefficient to leave the originating site. For example, if benzene n Na-Y (Si:Al=2.0) jumps from an SII site, the mean time elapsed is
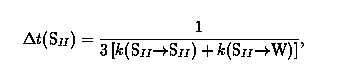
where the factor of three counts available target sites in the Na-Y supercage structure. Since rate coefficients for leaving the SII site are typically much smaller than those for leaving the WII site, the elapsed SII time is much larger than the elapsed WII time. Thus, the variable time step KMC random walk algorithm efficiently models both sluggish and rapid motions in the Na-Y--benzene system. Ensemble averages required for calculating mean square displacements are performed using multiple time origin averaging. In order to resolve translational dynamics over widely separated length and time scales we display mean square displacements with log-log plots. In these cases it is computationally advantageous to perform the ensemble average using logarithmic time bins.
Figure 7 shows how Na(II) occupancy varies with the Si:Al ratio in our model. We have calculated benzene diffusion coefficients for systems marked by circles (empty and filled) in Fig. 7 and have compared benzene mean square displacements to OCFs for systems marked by filled circles in Fig. 7. We note that by assuming full Na(I') occupancy for all Si:Al ratios, benzene mobility in our model increases precipitously near Si:Al=5.0 as the last Na(II) cation is removed. Such a sudden mobility increase is an artifact of our cation occupancy model, and is not to be taken seriously.
We model BOR in Na-Y for a given Si:Al ratio, and hence for a given Na(II) occupancy, by replacing the zeolite framework with a three-dimensional lattice of SII and W benzene binding sites, where the number of SII sites is obtained from Fig. 7. This model ignores benzene binding at supercage 6-rings with no associated Na(II) cation. This is a very good approximation because benzene residence times at these 6-rings are significantly shorter than the times required for full BOR. As such, benzene visiting 6-rings without Na(II) cations would contribute negligibly to the ensemble average in Eq. (0.2). From an experimental perspective, benzene rotational dynamics at these ``siliceous" 6-rings is too fast to be observed by two-dimensional exchange NMR, and is on the borderline for NMR relaxation.
Determining accurate spatial patterns of Na(II) occupancy for Na-Y (Si:Al>2.0) is challenging because of the difficulty in measuring and calculating Al and Na+ distributions in disordered zeolites. Since cation mobilities in dehydrated zeolites are significantly smaller than benzene mobilities, static on the time scale of BOR. We turn this difficulty to our advantage by proposing that benzene mobility can be used to probe static Na(II) disorder. That is, while we do not know the proper spatial Na(II) occupancy pattern, we can calculate benzene mobilities assuming various occupancy patterns to determine measurable signatures for these patterns.
We examine two such patterns below, both based on random Na(II) siting. The first pattern, called ``cage" disorder, assumes that each supercage has roughly the same number of Na(II) cations. For example, a Si:Al ratio of 3.0 gives on average two Na(II) cations per supercage. The cage disorder pattern requires that each supercage has exactly two Na(II) cations, placed randomly at two of the four possible tetrahedrally arranged sites. This pattern would arise physically from, e.g., a random distribution of framework Al with density fluctuations on a length scale smaller than the supercage dimension, and Na ions in close proximity to framework Al. Although this spatial distribution seems plausible, it imposes constraints which may be artificial. A less constrained pattern, called "cell" disorder, randomly places Na(II) cations in the Na-Y cubic unit cell.
Schematic illustrations of cage and cell disorder are shown in Figs. 8, 9 and 10. Figure 8 depicts the Na-Y (Si:Al=2.0) unit cell containing 8 supercages and 8 beta cages. The shaded boxes are beta cages containing no Na(II) cations, and the unshaded boxes are supercages containing four Na(II) cations (black dots) because Si:Al=2.0. Figure 9 shows cage disorder for Na-Y (Si:Al=3.0), with 16 Na(II) cations per unit cell randomly distributed so that each supercage contains two ions. Figure 10 shows cell disorder for Na-Y (Si:Al=3.0), involving 16 Na(II) cations randomly distributed over the unit cell, in this case giving one supercage with no Na(II) cations and one supercage with four cations. We emphasize that our KMC simulations of benzene in Na-Y (Si:Al>=2.0) use the actual Na-Y structure for constructing lattices of SII and W benzene binding sites.
We model benzene orientational randomization (BOR) in Na-Y for a given Si:Al ratio, and hence for a given Na(II) occupancy, by replacing the zeolite framework with a three-dimensional lattice of SII and W benzene binding sites where the number of SII sites is obtained from Fig. 7. SII sites are placed randomly according to either cage or cell disorder. We use fixed time step kinetic Monte Carlo (KMC) for calculating OCFs, and also variable time step KMC for calculating mean square displacements. The results are examined to determine which underlying jumps control BOR, the extent to which OCFs and mean square displacements contain complementary information, and the effect of static Na(II) disorder on benzene mobilities.